Two thousand years ago, the ancient Greeks looked into the night sky and saw geometric shapes emerge among the stars: a hunter, a lion, a water vase.
In a way, they used these constellations to make sense of the random scattering of stars in the fabric of the universe. By translating astronomy into shapes, they found a way to seek order and meaning in a highly complex system.
As it turns out, the Greeks were wrong: most stars in a constellation don’t have much to do with one another. But their approach lives on.
This week, the Blue Brain Project proposed a fascinating idea that may explain the complexities of the human brain. Using algebraic topology, a type of mathematics that “projects” complex connections into graphs, they mapped out a path for complex functions to emerge from the structure of neural networks.
And get this: while the brain physically inhabits our three-dimensional world, its inner connections—mathematically speaking—operate on a much higher dimensional space. In human speak: the assembly and disassembly of neural connections are massively complex, more so than expected. But now we may have a language to describe them.
“We found a world that we had never imagined,” says Dr. Henry Markram, director of Blue Brain Project and professor at the EPFL in Lausanne, Switzerland who led the study.
This may be why it’s been so difficult to understand the brain, he says. “The mathematics usually applied to study networks cannot detect the high-dimensional structures and spaces that we now see clearly.”
A high-dimensional world
When we think about the brain, branchy neurons and gooey tissue come to mind—definitely 3D objects. Physically speaking, there are no high-dimensional mini-brains hidden within our own, and our neurons don’t jump into a higher plane of existence when they fire away.
Outside of physics, “dimension” is really just a fancy way of describing complexity. Take a group of three neurons that work together (A, B, and C), for example. Now think about how many ways they can connect together. Because information is generally only passed one way from a neuron to its downstream partner, A can only link to B or C. In topology speak, the dimension here is two.
Similarly, a group of four neurons has dimension three, five neurons dimension four and so on. The more neurons in a group, the higher the dimension—and so the system gets increasingly complex.
“In our study, dimension does not describe spatial dimensions, but rather the topological dimension of the geometric objects we are describing. A 7- or 11-dimensional simplex is still embedded in the physical three-dimensional space,” explains study author Max Nolte, a graduate student at EPFL, to Singularity Hub.
Multi-dimensional connections
To begin parsing out the organization of the brain, the team started with functional building blocks called simplices. Each simplex is a special group of neurons connected with each other in a very specific order.
One neuron is very influential and speaks first, one listens to all neurons, and others listen to a few neurons and speak to the ones they’re not listening to, says Nolte. “This specific structure makes sure that the listening neurons can really understand the speaking neurons in a brain where always millions of neurons are talking at the same time, like in a crowded stadium.”
As before, dimensions describe the complexity of a simplex.
In six different virtual brains, each reconstructed from experimental data obtained in rats, the team looked for signs of these abstract mathematical objects. Incredibly, the virtual brains contained extremely complex simplices—up to dimension seven—and roughly 80 million lower dimensional neuron “groups.”
The enormous amount of simplices hidden inside the brain suggests that each neuron is a part of an immense number of functional groups, much more than previously thought, says Nolte.
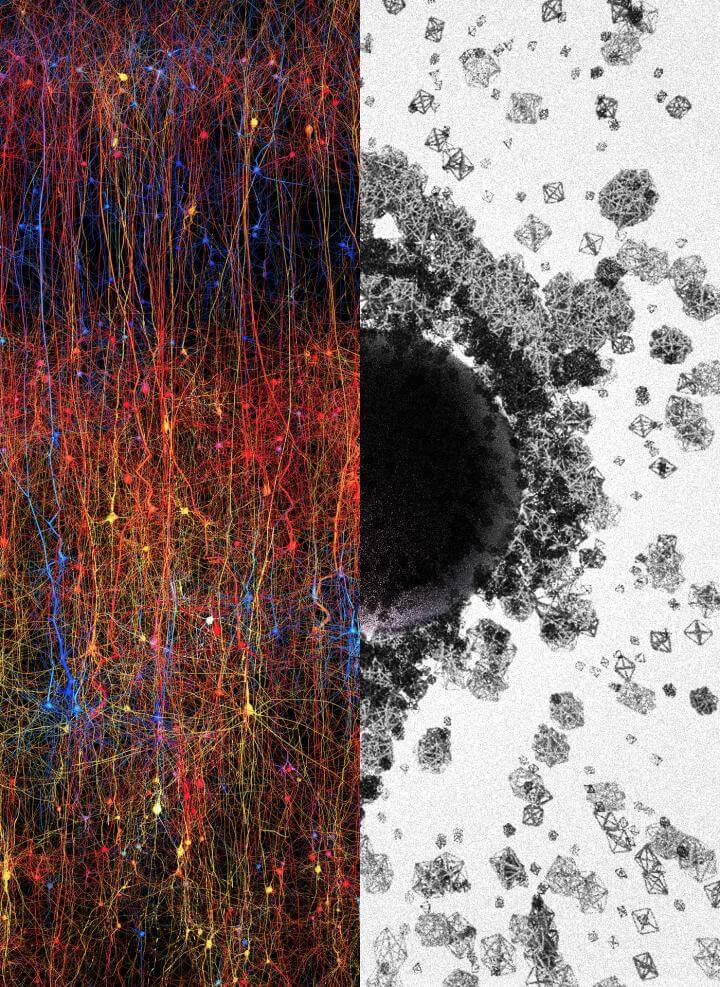
Emerging function
If simplices are building blocks, then how do they come together to form even more complicated networks?
When the team exposed their virtual brain to a stimulus, the neurons assembled into increasingly intricate networks, like blocks of Lego building a castle.
Again, it’s not necessarily a physical connection. Picture groups of neurons linking to others like a social graph, and the graphs associating into a web or other high-dimensional structure.
The fit wasn’t perfect: in between the higher-dimensional structures were “holes,” places where some connections were missing to make a new web.
Like simplices, holes also have dimensions. In a way, says Nolte, “the dimension of a hole describes how close the simplices were to reaching a higher dimension,” or how well the building blocks associated with each other.
The appearance of progressively higher dimensional holes tells us that neurons in the network respond to stimuli in an “extremely organized manner,” says Dr. Ran Levi at the University of Aberdeen, who also worked on the paper.
When we look at the reaction of the brain over time to a stimulus, we see abstract geometric objects forming and then falling apart as it builds functional networks, says Levi.
The brain first recruits simpler neural networks to build a 1D “frame.” These networks then associate into 2D “walls” with “holes” in between. Fast-forward and increasingly higher dimensional structures and holes form, until they reach peak organization—whatever connections the neurons need to get the job done.
Once there, the entire structure collapses, freeing up the simplices for their next tasks, like sand castles materializing and then disintegrating away.
“We don’t know…what the brain is doing when it forms these cavities,” says Levi to Singularity Hub.
What’s clear, however, is that neurons have to fire in a “fantastically ordered” manner for these high-dimensional structures to occur.
“It is quite clear that this hyper-organized activity is not just a coincidence. This could be the key to understanding what is going on when the brain is active,” says Levi.
Talking in sync
The team also worked out how neurons in the same or different groups talked to one another after a stimuli.
It really depends on where they are in the high-dimensional structure and their own groups.
Imagine two “stranger” neurons chatting away, says Nolte. They’ll probably say many unrelated things, because they don’t know each other.
Now, imagine after a stimulus they form high-dimensional networks. Like Twitter, the network allows one neuron to hear the other, and they may begin repeating some of the things the other one said. If they both follow dozens of other people, their tweets may be even more similar because their thoughts are influenced by a shared crowd.
“Using simplices, we don’t only count how many shared people they are following, but also how these people they are following are connected to each other,” says Nolte. The more interconnected two neurons are—that is, the more simplices they are a part of—the more they fire to a stimulus in the same way.
It really shows the importance of the functional structure of the brain, in that structure guides the emergence of correlated activity, says Levi.
Previous studies have found that the physical structure of neurons and synapses influence activity patterns; now we know that their connections in “high-dimensional space” also factor in.
Going forward, the team hopes to understand how these complicated, abstract networks guide our thinking and behaviors.
“It’s like finding a dictionary that translates a totally obscure language to another language that we are actually familiar with, even if we don’t necessarily understand all stories written in this language,” says Levi.
Now it’s time to decipher those stories, he adds.
Image credit: Shutterstock